This section describes the working of Turf.js module Along.
Purpose of this Turf.js module
This takes a LineString as an input and returns a point at a specified distance from the starting. For more information and its usage visit its official documentation page.
Pre-requisites for understanding this module
-
Haversine Formula and its Arctangent version
- Basically, this formula calculates distance between two points over a spherical surface.
-
Measurement of angles in Radians
- It is more natural to measure angles in radians than in degrees. Most of the calculations here are done in Radians.
-
Concept of Bearing
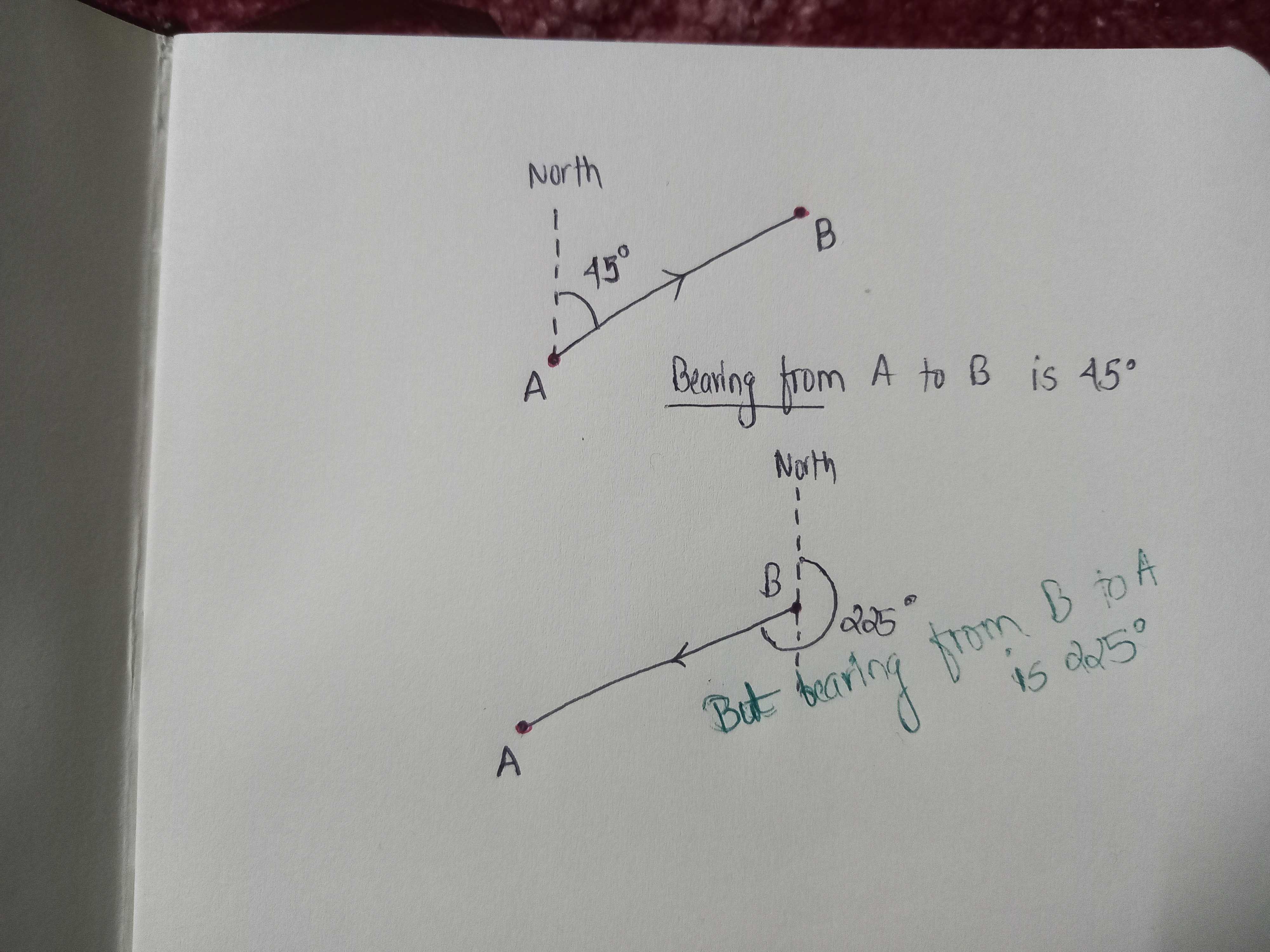
- Bearing is the angle that a line segment AB (or BA) makes with the North direction (considered 0°). As in the figure, if Bearing from A to B is 45°, then bearing from B to A is 225°.
Behind the scenes- Working of this module
Variables/Assumptions
- Distance to travel from the starting point in KM = d
- Total distance travelled since starting point in KM = t
Cases
There are various cases of this.
Case-1
-
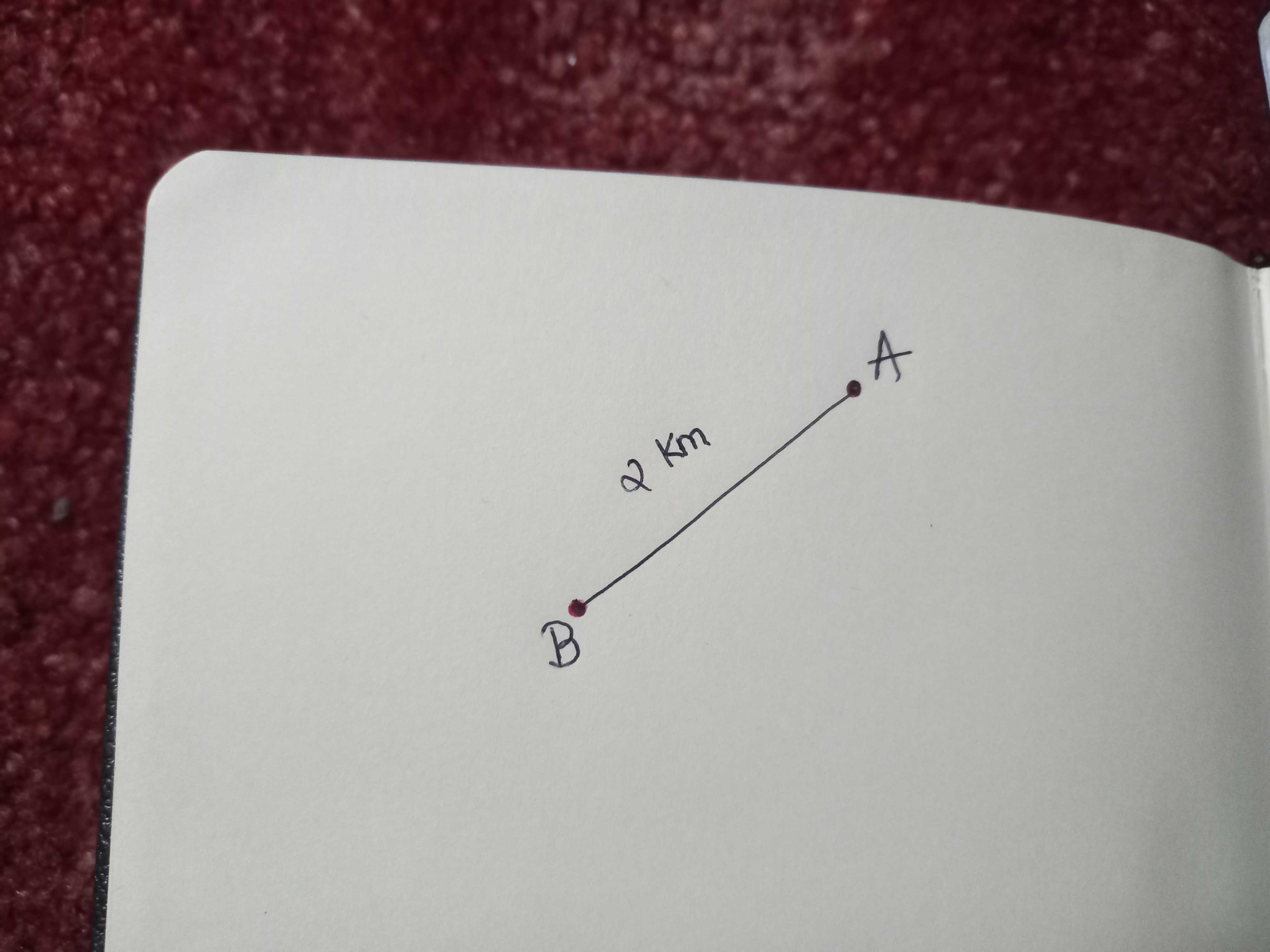
Let us consider the following diagram.
-
Let say we have d = 4. At A, t=0. We travel from point A to point B and measure its distance using Haversine formula from A to B.
-
At B, distance from A to B = 2 KM, then we dont need any further calculation (because d=4 KM and the total travelable distance is just 2KM).
-
So, B is the point itself.
Case-2
-
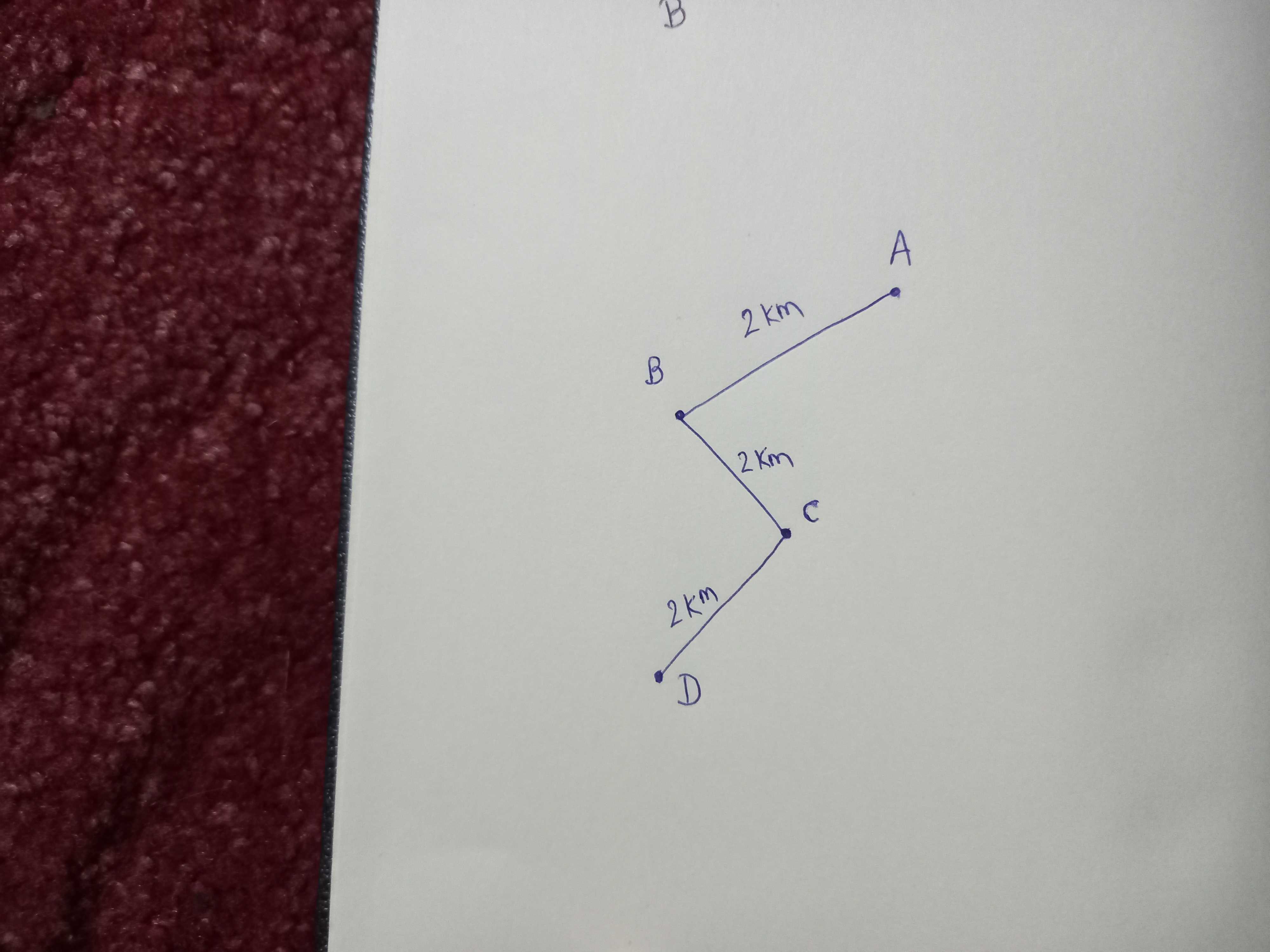
Now let us consider another diagram with point ABCD.
-
At B, we have travelled just 2 KM. If d > 2 KM, we need to go a little further. We travel from B to C and update the t.
-
At C, we have covered 4 KM. If d is more than 4 KM, we continue moving forward to another point.
Case-3
-
Let’s revisit the Case-2. Here, lets say we have d=3.5 KM.
-
At C, we have already covered 4 KM. Thus, we need to go (4-3.5) KM back along CB at some angle. So what is that angle?
-
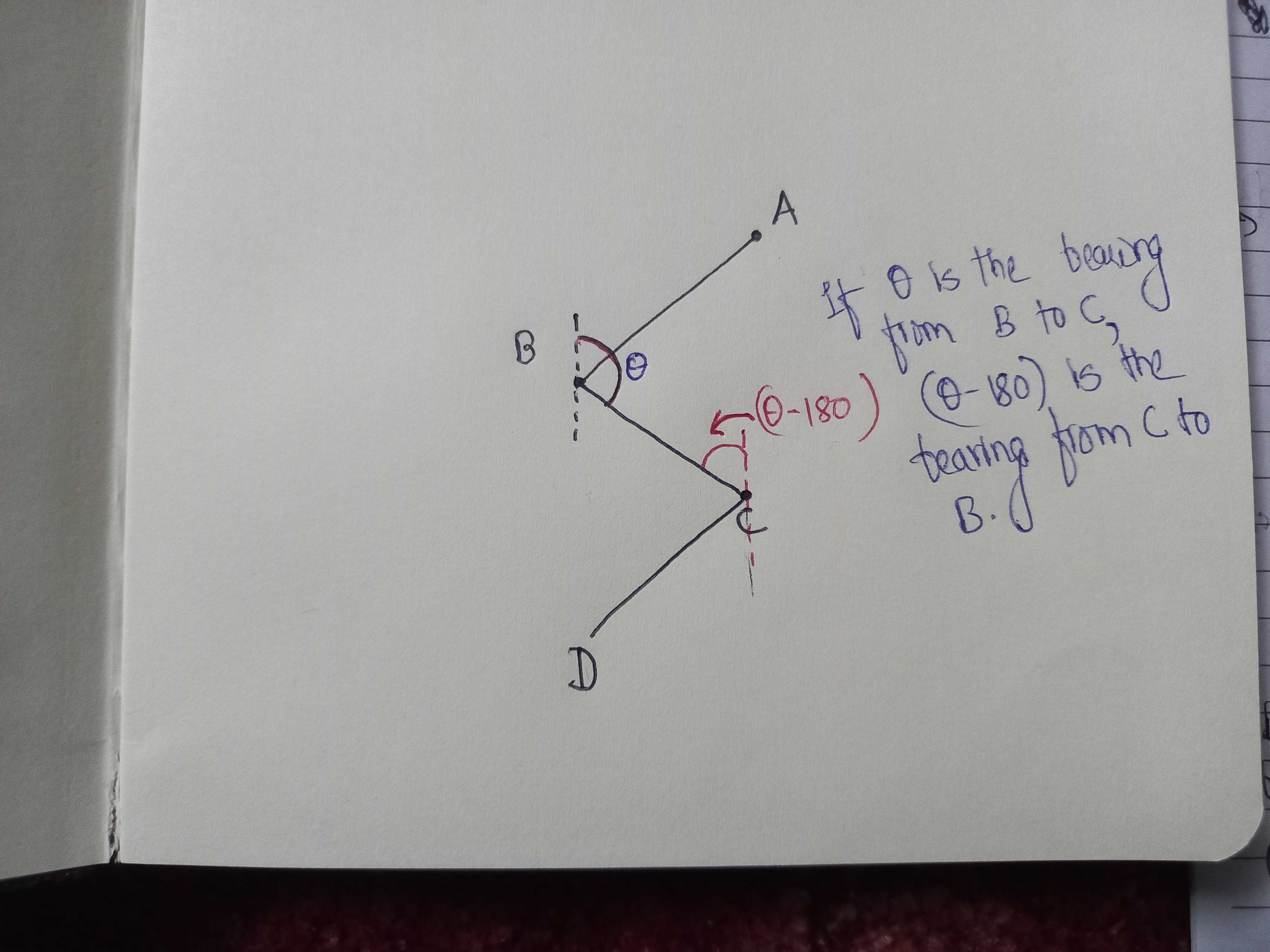
It is the bearing that we have going from C to B. As in the figure, if θ is the bearing from B to C, θ-180 is the bearing from C to B.
-
Note that, here bearing is considered only within the range -180 to + 180.
-
After that, we just traverse back 1.5 KM along the path CB, at bearing of θ-180 using interpolation (based on Haversine formula) to find the final point.